The DTW project has a new home!

Welcome to the Dynamic Time Warp project!

The R Package dtw provides the most complete, freely-available (GPL) implementation of Dynamic Time Warping-type (DTW) algorithms up to date.

The package is described in a companion paper, including detailed instructions and extensive background on things like multivariate matching, open-end variants for real-time use, interplay between recursion types and length normalization, history, etc.

Description

DTW is a family of algorithms which compute the local stretch or compression to apply to the time axes of two timeseries in order to optimally map one (query) onto the other (reference). DTW outputs the remaining cumulative distance between the two and, if desired, the mapping itself (warping function). DTW is widely used e.g. for classification and clustering tasks in econometrics, chemometrics and general timeseries mining.

The R implementation in dtw provides:

• arbitrary windowing functions (global constraints), eg. the Sakoe-Chiba band and the Itakura parallelogram;
• arbitrary transition types (also known as step patterns, slope constraints, local constraints, or DP-recursion rules). This includes dozens of well-known types:
  • all step patterns classified by Rabiner-Juang, Sakoe-Chiba, and Rabiner-Myers;
  • symmetric and asymmetric;
  • Rabiner's smoothed variants;
  • arbitrary, user-defined slope constraints
• partial matches: open-begin, open-end, substring matches
• proper, pattern-dependent, normalization (exact average distance per step)
• the Minimum Variance Matching (MVM) algorithm (Latecki et al.)

Multivariate timeseries can be aligned with arbitrary local distance definitions, leveraging the {proxy}dist function. DTW itself becomes a distance function with the dist semantics.

In addition to computing alignments, the package provides:

• methods for plotting alignments and warping functions in several classic styles (see plot gallery);
• graphical representation of step patterns;
• functions for applying a warping function, either direct or inverse;
• both fast native (C) and interpreted (R) cores.

Documentation

The best place to learn how to use the package (and a hopefully a decent deal of background on DTW) is the companion paper Computing and Visualizing Dynamic Time Warping Alignments in R: The dtw Package, which the Journal of Statistical Software makes available for free.

To have a look at how the dtw package is used in domains ranging from bioinformatics to chemistry to data mining, have a look at the list of citing papers.

A link to prebuilt documentation is here.

Citation

If you use dtw, do cite it in any publication reporting results obtained with this software. Please follow the directions given in citation("dtw"), i.e. cite:

Toni Giorgino (2009). Computing and Visualizing Dynamic Time Warping Alignments in R: The dtw Package. Journal of Statistical Software, 31(7), 1-24, doi:10.18637/jss.v031.i07.

When using partial matching (unconstrained endpoints via the open.begin/open.end options) and/or normalization strategies, please also cite:

Paolo Tormene, Toni Giorgino, Silvana Quaglini, Mario Stefanelli (2008). Matching Incomplete Time Series with Dynamic Time Warping: An Algorithm and an Application to Post-Stroke Rehabilitation. Artificial Intelligence in Medicine, 45(1), 11-34. doi:10.1016/j.artmed.2008.11.007

Plot gallery

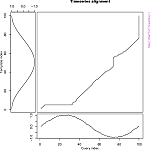
Go to a gallery of sample plots (straight out of the examples in the documentation).

Quickstart Example

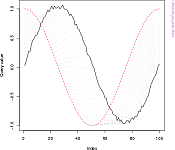
## A noisy sine wave as query
idx<-seq(0,6.28,len=100);
query<-sin(idx)+runif(100)/10;

## A cosine is for template; sin and cos are offset by 25 samples
template<-cos(idx)

## Find the best match with the canonical recursion formula
library(dtw);
alignment<-dtw(query,template,keep=TRUE);

## Display the warping curve, i.e. the alignment curve
plot(alignment,type="threeway")

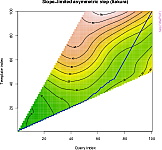
## Align and plot with the Rabiner-Juang type VI-c unsmoothed recursion
plot(
    dtw(query,template,keep=TRUE,
        step=rabinerJuangStepPattern(6,"c")),
    type="twoway",offset=-2);

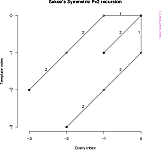
## See the recursion relation, as formula and diagram
rabinerJuangStepPattern(6,"c")
plot(rabinerJuangStepPattern(6,"c"))

## And much more!  
Try online

Installation

To install the latest stable build of the package (hosted at CRAN), issue the following command in the R console:

> install.packages("dtw")

To get started, begin from the installed documentation:

> library(dtw) 
> demo(dtw)
> ?dtw 
> ?plot.dtw

Frequently asked questions

Alas, most likely you haven't. DTW had been "multidimensional" since its conception. Local distances are computed between N-dimensional vectors; feature vectors have been extensively used in speech recognition since the '70s (see e.g. things like MFCC, RASTA, cepstrum, etc). Don't worry: several other people have "rediscovered" multivariate DTW already. The dtw package supports the numerous types of multi-dimensional local distances that the proxy package does, as explained in section 3.6 of the paper in JSS.

Alas, most likely you haven't. A natural solution for real-time recognition of timeseries is "unconstrained DTW", which relaxes one or both endpoint boundary conditions. To my knowledge, the algorithm was published as early as 1978 by Rabiner, Rosenberg, and Levinson under the name UE2-1: see e.g. the mini-review in (Tormene and Giorgino, 2008). Feel also free to learn about the clever algorithms or expositions by Sakurai et al. (2007); Latecki (2007); Mori et al. (2006); Smith-Waterman (1981); Rabiner and Schmidt (1980); etc. Open-ended alignments (at one or both ends) are available in the dtw package, as described in section 3.5 of the JSS paper.

Alas, most likely you haven't. You may be doing backtracking via steepest descent. It's not the correct way to do it. Here's a counterexample:

> library(dtw) 
> dm<-matrix(10,4,4)+diag(rep(1,4))
> al<-dtw(dm,k=T,step=symmetric2) 	
> al$localCostMatrix
      [,1] [,2] [,3] [,4]
[1,]   11   10   10   10
[2,]   10   11   10   10
[3,]   10   10   11   10
[4,]   10   10   10   11
> al$costMatrix
      [,1] [,2] [,3] [,4]
[1,]   11   21   31   41
[2,]   21   32   41   51
[3,]   31   41   52   61
[4,]   41   51   61   72
	  

The sum of costs along my warping path (blue) is (starting from [1,1]) 11+10+2*10+2*10+11 = 72 which is correct (=g[4,4]) . If you follow your backtracking "steepest descent" algorithm (red), you get the diagonal 11+2*11+2*11+2*11=77 which is wrong.

An alignment computed with a non-normalizable step pattern has two serious drawbacks:

1. It cannot be meaningfully normalized by timeseries length. Hence, longer timeseries have naturally higher distances, in turn making comparisons impossible.
2. It favors diagonal steps, therefore it is not robust: two paths differing for a small local change (eg. horizontal+vertical step rather than diagonal) have very different costs.

This is discussed in section 3.2 of the JSS paper, section 4.2 of the AIIM paper, section 4.7 of Rabiner and Juang's Fundamentals of speech recognition book, and elsewhere. Make sure you familiarize yourself with those references.

TLDR: just stick to the default symmetric2 recursion and use the value of normalizedDistance.

(New!). Yes! You can now use the dtw-python package, which is closely modeled after the R one.

In the past, I recommended Stefan Novak's version of the quickstart example on Stack Overflow (reported here in updated form). The mapping was performed through the Python package rpy2, which makes the code natural and readable. It also reportedly plays well with numpy, pandas and multiprocessing.

import numpy as np

import rpy2.robjects.numpy2ri
from rpy2.robjects.packages import importr
rpy2.robjects.numpy2ri.activate()
    
# Set up our R namespaces
R = rpy2.robjects.r
DTW = importr('dtw')

# Generate our data
idx = np.linspace(0, 2*np.pi, 100)
template = np.cos(idx)
query = np.sin(idx) + np.random.uniform(size=100)/100.

# Calculate the alignment vector and corresponding distance
alignment = R.dtw(query, template, keep=True)
dist = alignment.rx('distance')[0][0]

print(dist)

See command diff.

This question has been raised on Stack Overflow; see here, here and here. A good first guess is symmetric2 (the default), i.e.

	     g[i,j] = min(
	         g[i-1,j-1] + 2 * d[i  ,j  ] ,
	         g[i  ,j-1] +     d[i  ,j  ] ,
	         g[i-1,j  ] +     d[i  ,j  ] ,
	     )
	 

There are two very different, totally unrelated uses for dist. This is explained at length in the paper, but let's summarize.

1. If you have two multivariate timeseries, you can feed them to dist to obtain a local distance matrix. You then pass this matrix to dtw(). This is equivalent to passing the two matrices to the dtw() function and specifying a dist.method (see also the next question).
2. If you have many univariate timeseries, instead of iterating over all pairs and applying dtw() to each, you may feed the lot (arranged as a matrix) to dist with method="DTW". In this case your code does NOT explicitly call dtw(). This is equivalent to iterating over all pairs; it is also equivalent to using the dtwDist convenience function.

Because it only makes a difference when aligning multivariate timeseries. It specifies the "pointwise" or local distance used (before the alignment) between the query feature vector at time i, query[i,] and the reference feature vector at time j, ref[j,] . Most distance functions coincide with the Euclidean distance in the one-dimensional case. Note the following:

r<-matrix(runif(10),5)  # A 2-D timeseries of length 5
s<-matrix(runif(10),5)  # Ditto

myMethod<-"Manhattan" # Or anything else
al1<-dtw(r,s,dist.method=myMethod)              # Passing the two inputs
al2<-dtw(proxy::dist(r,s,method=myMethod))      # Equivalent, passing the distance matrix

all.equal(al1,al2) 
     

The first thing you should try is to set the distance.only=TRUE parameter, which skips backtracing and some object copies. Second, consider downsampling the input timeseries.

Clustering FAQ

Of course. You need to start with a dissimilarity matrix, i.e. a matrix holding in i,j the DTW distance between timeseries i and j. This matrix is fed to the clustering functions. Obtaining the dissimilarity matrix is done differently depending on whether your timeseries are univariate or or multivariate: see the next questions.

Arrange the timeseries (single-variate) in a matrix as rows. Make sure you use a symmetric pattern. See dtwDist.

You have to handle the loop yourself. Assuming you have data arranged as x[time,component,series], pseudocode would be:

 for (i in 1:N) { 
    for (j in 1:N) { 
        result[i,j] <- dtw( dist(x[,,i],x[,,j]), distance.only=T )$normalizedDistance 

Either loop over the inputs yourself, or pad with NAs and use the following code:

dtwOmitNA <-function (x,y)
{
    a<-na.omit(x)
    b<-na.omit(y)
    return(dtw(a,b,distance.only=TRUE)$normalizedDistance)
}

## create a new entry in the registry with two aliases
pr_DB$set_entry(FUN = dtwOmitNA, names = c("dtwOmitNA"))

d<-dist(dataset, method = "dtwOmitNA") 

License

This software is distributed under the terms of the GNU General Public License Version 2, June 1991. The terms of this license are in a file called COPYING which you should have received with this software and which can be displayed by RShowDoc("COPYING").

Contact

Commercial support

I am also interested in hearing from companies seeking to use DTW in a commercial setting. I may provide on-site and/or remote consultancy through the Istituto di Biofisica.